Estructuras dinámicas de datos. Capítulo 008d

8.8 Algoritmos

De inserción de nodo

En general, la inserción de nodos en un árbol AVL es igual que en un árbol ABB, la diferencia es que en un árbol AVL, después de insertar el nodo debemos recorrer el árbol en sentido hacia la raíz, recalculando los valores de FE, hasta que se cumpla una de estas condiciones: que lleguemos a la raíz, que se encuentre un nodo con valor de FE de 2, ó -2, o que se llegue a un nodo cuyo FE no cambie o decrezca en valor absoluto, es decir, que cambie de 1 a 0 ó de -1 a 0.

Podemos considerar que el algoritmo de inserción de nodos en árboles AVL es una ampliación del que vimos para árboles ABB.

De borrado de nodo

Lo mismo pasa cuando se eliminan nodos, el algoritmo es el mismo que en árboles ABB, pero después de eliminar el nodo debemos recorrer el camino hacia la raíz recalculando los valores de FE, y equilibrando el árbol si es necesario.

De recalcular FE

Ya comentamos más atrás que para seguir el camino desde el nodo insertado o borrado hasta el nodo raíz tenemos dos alternativas:

Guardar en una pila los punteros a los nodos por los que hemos pasado para llegar al nodo insertado o borrado, es decir, almacenar el camino.
Añadir un nuevo puntero a cada nodo que apunte al padre del nodo actual. Esto nos permite recorrer el árbol en el sentido contrario al normal, es decir, en dirección a la raíz.

Para calcular los nuevos valores de FE de los nodos del camino hay que tener en cuenta los siguientes hechos:

El valor de FE de un nodo insertado es cero, ya que siempre insertaremos nodos hoja.
Si el nuevo valor de FE para cualquiera de los siguientes nodos del camino es cero, habremos terminado de actualizar los valores de FE, ya que la rama mantiene su altura, la inserción o borrado del nodo no puede influir en los valores de FE de los siguientes nodos del camino.
Cuando se elimine un nodo pueden pasar dos cosas. Siempre eliminamos un nodo hoja, ya que cuando no lo es, lo intercambiamos con un nodo hoja antes de eliminarlo. Pero algunas veces, el nodo padre del nodo eliminado se convertirá a su vez en nodo hoja, y en ese caso no siempre hay que dar por terminada la actualización del FE del camino. Por lo tanto, cuando eliminemos un nodo, actualizaremos el valor de FE del nodo padre y continuaremos el camino, independientemente del valor de FE calculado.
A la hora de actualizar el valor de FE de un nodo, tenemos que distinguir cuando el equilibrado sea consecuencia de una inserción o lo sea de una eliminación. Incrementaremos el valor de FE del nodo si la inserción fue en la rama derecha o si la eliminación fue en la rama izquierda, decrementaremos si la inserción fue en la izquierda o la eliminación en la derecha.
Si en valor de FE es -2, haremos una rotación doble a la derecha su el valor de FE del nodo izquierdo es 1, y simple si es 1 ó 0.
Si en valor de FE es 2, haremos una rotación doble a la izquierda su el valor de FE del nodo izquierdo es -1, y simple si es -1 ó 0.
En cualquiera de los dos casos, podremos dar por terminado el recorrido del camino, ya que la altura del árbol cuya raíz es un nodo rotado no cambia.
En cualquier otro caso, seguiremos actualizando hasta llegar al nodo raíz.

De rotación simple

A la hora de implementar los algoritmos que hemos visto para rotaciones simples tenemos dos opciones: seguir literalmente los pasos de los gráficos, o tomar un atajo, y hacerlo mediante asignaciones. Nosotros lo haremos del segundo modo, ya que resulta mucho más rápido y sencillo.

Primero haremos las reasignaciones de punteros, de modo que el árbol resultante responda a la estructura después de la rotación. Después actualizaremos los punteros al nodo padre para los nodos que han cambiado de posición. Por último actualizaremos los valores de FE de esos mismos nodos.

Para la primera fase usaremos punteros auxiliares a nodo, que en el caso de rotación a la derecha necesitamos un puntero P al nodo con FE igual a -2. Ese será el parámetro de entrada, otro puntero al nodo izquierdo de P: Q. Y tres punteros más a los árboles A, B y C.

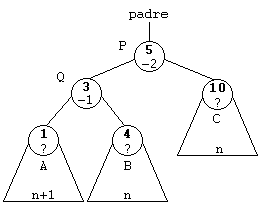
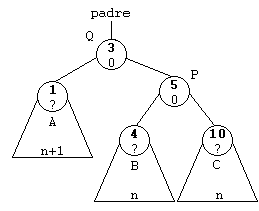
En realidad, si nos fijamos en los gráficos, los punteros a A y C no son necesarios, ya que ambos conservan sus posiciones, A sigue siendo el subárbol izquierdo de Q y C el subárbol derecho de P.

Usaremos otro puntero más: Padre, que apunte al padre de P. Disponiendo de los punteros Padre, P, Q y B, realizar la rotación es muy sencillo:

   if(Padre) 
     if(Padre->derecho == P) Padre->derecho = Q;
     else Padre->izquierdo = Q;
   else raíz = Q;

   // Reconstruir árbol:
   P->izquierdo = B;
   Q->derecho = P;

Hay que tener en cuenta que P puede ser la raíz de un subárbol derecho o izquierdo de otro nodo, o incluso la raíz del árbol completo. Por eso comprobamos si P tiene padre, y si lo tiene, cual de sus ramas apunta a P, cuando lo sabemos, hacemos que esa rama apunte a Q. Si Padre es NULL, entonces P era la raíz del árbol, así que hacemos que la nueva raíz sea Q.

Sólo nos queda trasladar el subárbol B a la rama izquierda de P, y Q a la rama derecha de P.

La segunda fase consiste en actualizar los punteros padre de los nodos que hemos cambiado de posición: P, B y Q.

   P->padre = Q;
   if(B) B->padre = P;
   Q->padre = Padre;

El padre de P es ahora Q, el de Q es Padre, y el de B, si existe es P.

La tercera fase consiste en ajustar los valores de FE de los nodos para los que puede haber cambiado.

Esto es muy sencillo, después de una rotación simple, los únicos valores de FE que cambian son los de P y Q, y ambos valen 0.

// Rotación simple a derechas
void RSD(Nodo* nodo) {
   Nodo *Padre = nodo->padre;
   Nodo *P = nodo;
   Nodo *Q = P->izquierdo;
   Nodo *B = Q->derecho;

   if(Padre) 
     if(Padre->derecho == P) Padre->derecho = Q;
     else Padre->izquierdo = Q;
   else raíz = Q;

   // Reconstruir árbol:
   P->izquierdo = B;
   Q->derecho = P;
   
   // Reasignar padres:
   P->padre = Q;
   if(B) B->padre = P;
   Q->padre = Padre;

   // Ajustar valores de FE:
   P->FE = 0;
   Q->FE = 0;
}

La rotación a izquierdas es simétrica.

De rotación doble

Para implementar las rotaciones dobles trabajaremos de forma análoga.

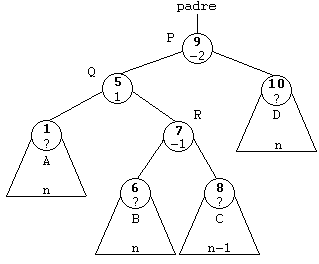
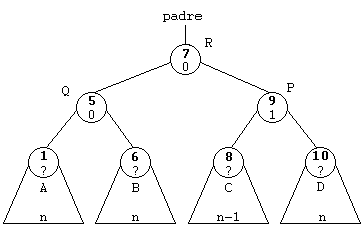
En realidad, si nos fijamos en los gráficos, los punteros a A y D no son necesarios, ya que ambos conservan sus posiciones, A sigue siendo el subárbol izquierdo de Q y D el subárbol derecho de P.

También en este caso usaremos otro puntero más: Padre, que apunte al padre de P. Disponiendo de los punteros Padre, P, Q, R, B y C, realizar la rotación es muy sencillo:

   if(Padre) 
     if(Padre->derecho == nodo) Padre->derecho = R;
     else Padre->izquierdo = R;
   else raíz = R;

   // Reconstruir árbol:
   Q->derecho = B;
   P->izquierdo = C;
   R->izquierdo = Q;
   R->derecho = P;

Ahora también hay que tener en cuenta que P puede ser la raíz de un subárbol derecho o izquierdo de otro nodo, o incluso la raíz del árbol completo. Por eso comprobamos si P tiene padre, y si lo tiene, cual de sus ramas apunta a P, cuando lo sabemos, hacemos que esa rama apunte a R. Si Padre es NULL, entonces P era la raíz del árbol, así que hacemos que la nueva raíz sea R.

Sólo nos queda trasladar el subárbol B a la rama derecha de Q, C a la rama izquierda de P, Q a la rama izquierda de R y P a la rama derecha de R.

La segunda fase consiste en actualizar los punteros padre de los nodos que hemos cambiado de posición: P, Q, R, B y C.

   R->>padre = Padre;
   P->padre = Q->padre = R;
   if(B) B->padre = Q;
   if(C) C->padre = P;

El padre de R es ahora Padre, el de P y Q es R, y el de B, si existe es Q, y el de C, si existe, es P.

La tercera fase consiste en ajustar los valores de FE de los nodos para los que puede haber cambiado.

En las rotaciones dobles esto se complica un poco ya que puede suceder que el valor de FE de R antes de la rotación sea -1, 0 o 1. En cada caso, los valores de FE de P y Q después de la rotación serán diferentes.

   // Ajustar valores de FE:
   switch(R->FE) {
      case -1: Q->FE = 0; P->FE = 1; break;
      case 0:  Q->FE = 0; P->FE = 0; break;
      case 1:  Q->FE = -1; P->FE = 0; break;
   }
   R->FE = 0;

Si la altura de B es n-1 y la de C es n, el valor de FE de R es 1. Después de la rotación, la rama B pasa a ser el subárbol derecho de Q, por lo tanto, la FE de Q, dado que la altura de su rama izquierda es n, será 0. La rama C pasa a ser el subárbol izquierdo de P, y dado que la altura de la rama derecha es n, la FE de P será -1.

Si la altura de B es n y la de C es n-1, el valor de FE de R es -1. Después de la rotación, la rama B pasa a ser el subárbol derecho de Q, por lo tanto, la FE de Q, dado que la altura de su rama izquierda es n, será 0. La rama C pasa a ser el subárbol izquierdo de P, y dado que la altura de la rama derecha es n, la FE de P será 0.

Por último, si la altura de B y C es n, el valor de FE de R es 0. Después de la rotación, la rama B pasa a ser el subárbol derecho de Q, por lo tanto, la FE de Q, dado que la altura de su rama izquierda es n, será 0. La rama C pasa a ser el subárbol izquierdo de P, y dado que la altura de la rama derecha es n, la FE de P será 0.

// Rotación doble a derechas
void RDD(Nodo* nodo) {
   Nodo *Padre = nodo->padre;
   Nodo *P = nodo;
   Nodo *Q = P->izquierdo;
   Nodo *R = Q->derecho;
   Nodo *B = R->izquierdo;
   Nodo *C = R->derecho;

   if(Padre) 
     if(Padre->derecho == nodo) Padre->derecho = R;
     else Padre->izquierdo = R;
   else raíz = R;

   // Reconstruir árbol:
   Q->derecho = B;
   P->izquierdo = C;
   R->izquierdo = Q;
   R->derecho = P;
   
   // Reasignar padres:
   R->padre = Padre;
   P->padre = Q->padre = R;
   if(B) B->padre = Q;
   if(C) C->padre = P;

   // Ajustar valores de FE:
   switch(R->FE) {
      case -1: Q->FE = 0; P->FE = 1; break;
      case 0:  Q->FE = 0; P->FE = 0; break;
      case 1:  Q->FE = -1; P->FE = 0; break;
   }
   R->FE = 0;
}